NMR-TUTORIAL GUIDE_2.0
NMR EXPERIMENTS
 | In this section the following topics will be discussed: |
WHAT IS NMR
Chemical shifts and any kind of spin-spin couplings are most likely the most important features affecting the appearance of NMR spectra:
CHECK IT: | Marvel at the following video (BRUKER) demonstrating how in a simple 1H NMR experiment applied to ethanol 1H chemical shifts and (indirect) homonuclear couplings JHH become manifest in the respective 1H NMR spectrum. Note that a registration/login will be requested. Activate full screen mode and start the video. |
 | 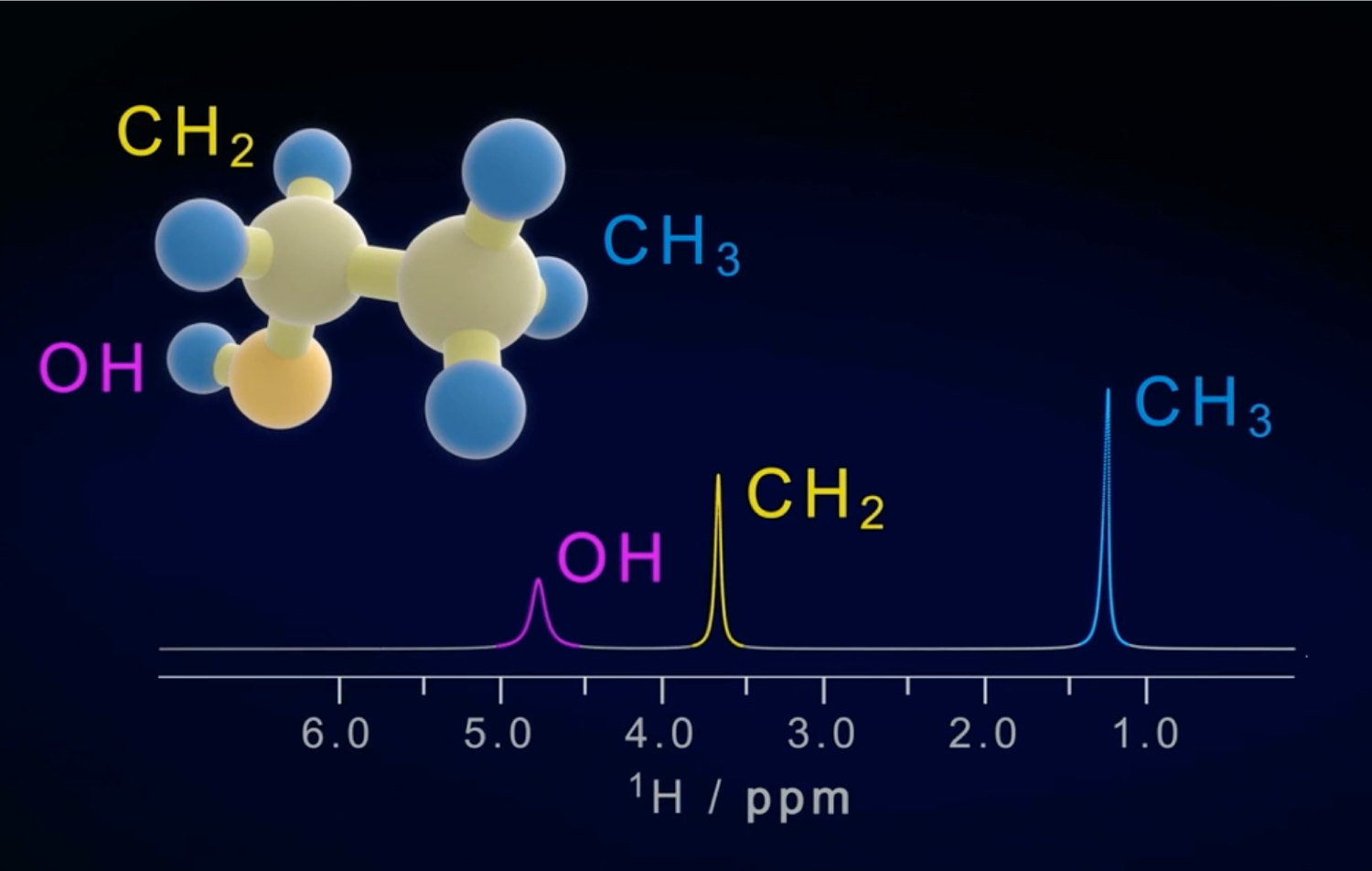 |
 | For a more comprehensive description of the essence of NMR the user is referred to: BRUKER AVANCE NEO BEGINNERS GUIDE FOR TOPSPIN USERS (pdf) Introductory Theory and Terminology: Navigate to chapter 3 | |
BACK TO: |
CLASSIFICATION OF NMR EXPERIMENTS
- their scope of application, e.g. experiments dedicated for small molecules/large molecules (biomolecules) or for liquid/semi-liquid/solid samples
- their parameter focus, e.g. experiments for measuring heteronuclear coupling constants or for detecting NOE interactions
- the experiments structure and elements (technical criteria classification)
A classification according to technical criteria is given below:
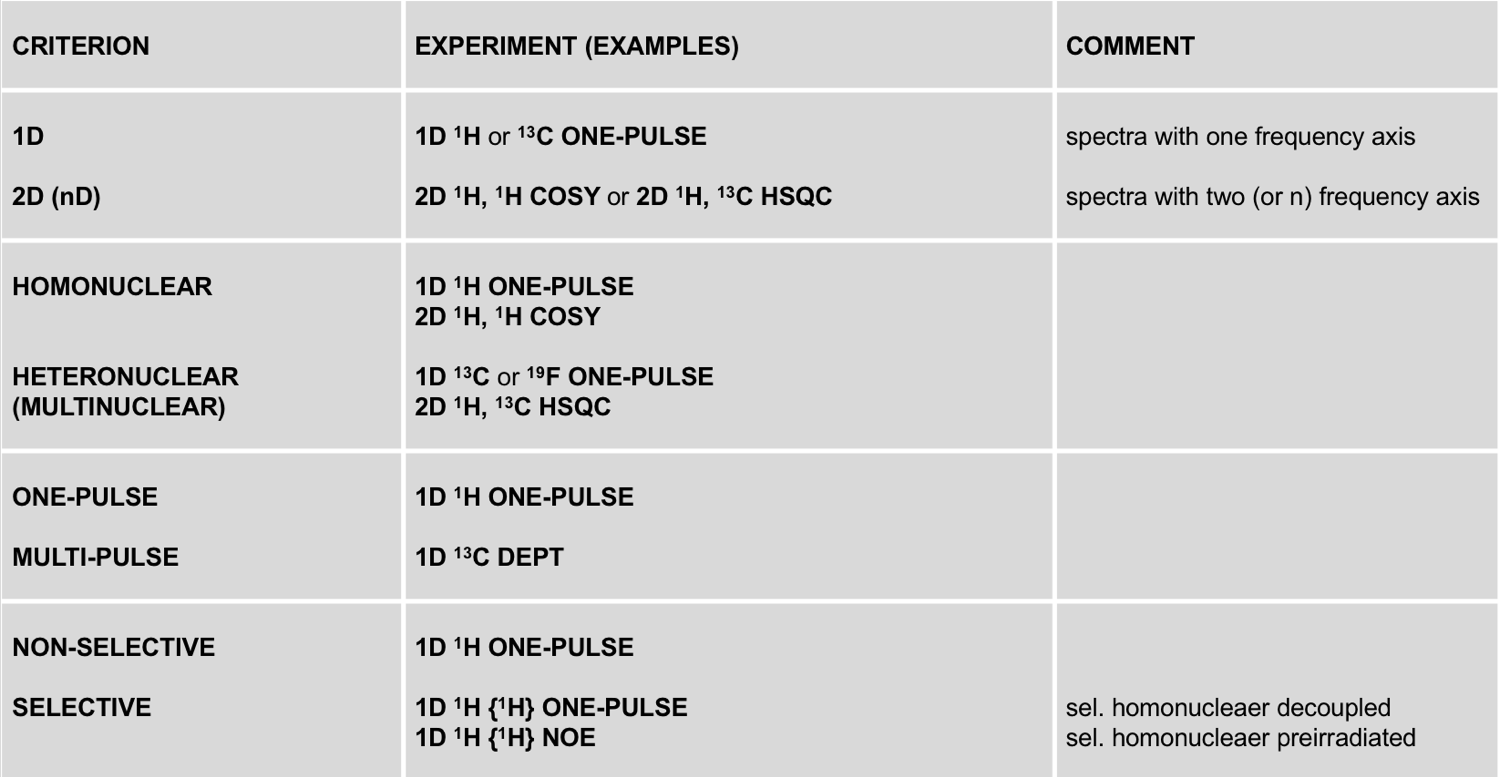
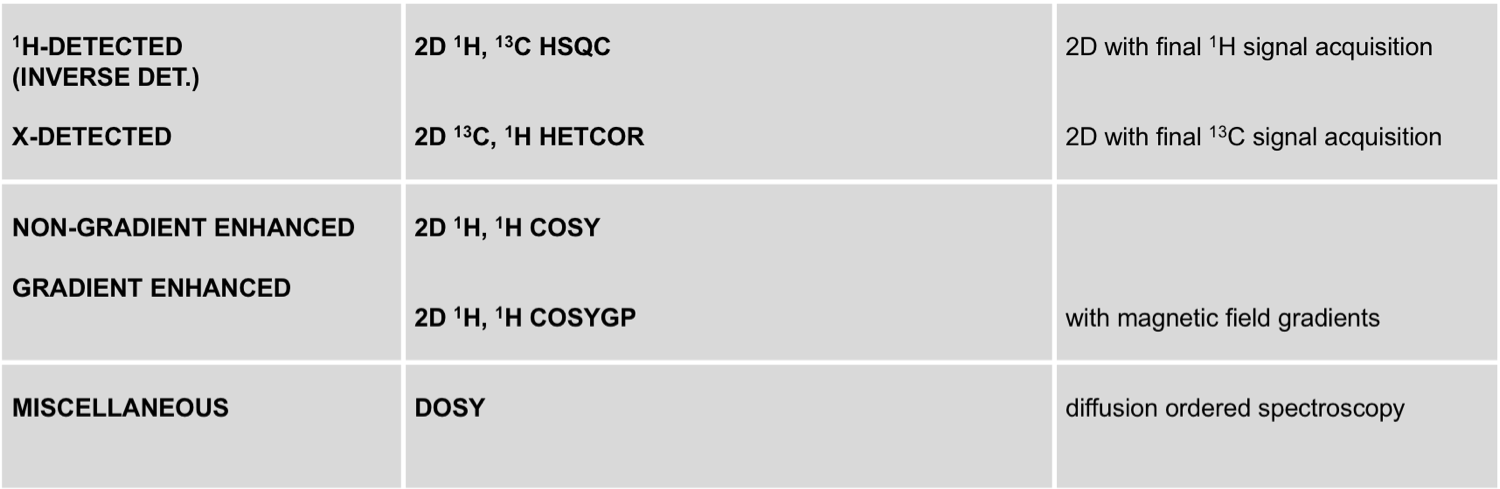
BACK TO: |
DIMENSIONALITY (1D, 2D) OF NMR EXPERIMENTS
The most important technical criterion for classifying NMR experiments is undoubtedly their dimensionality.
Basically and most frequently, two types of NMR experiments – 1D and 2D – are performed for routine applications.
As typical representatives the corresponding schemes of the 1D 1H ONE-PULSE experiment and the 2D 1H, 1H COSY experiment are shown below:
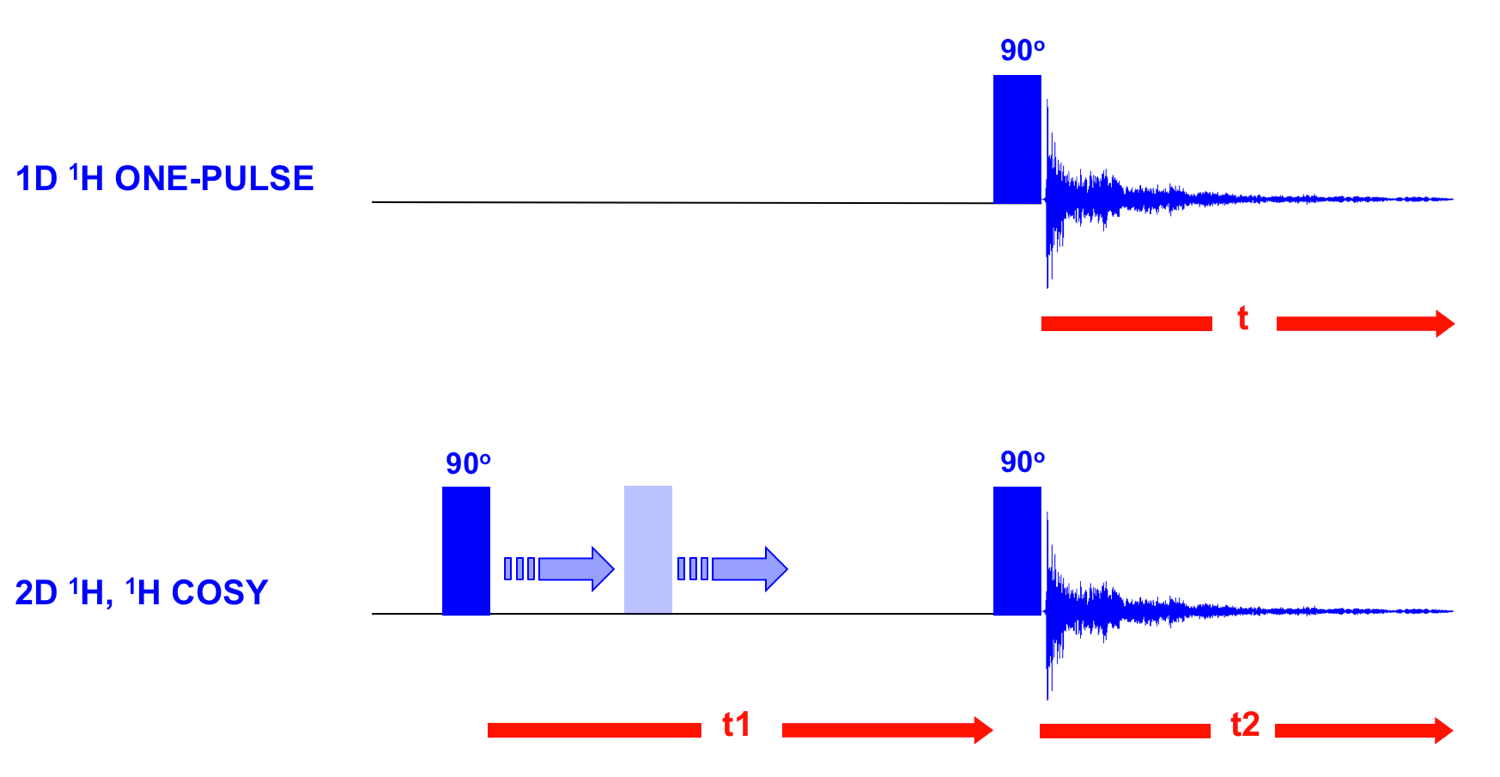 |
With 1D experiments a single experiment is performed with the signal intensity acquired along one time-axis t (the acquisition time).
With 2D experiments on the other hand a series of sub-experiments with one (or more) delays incremented in a second time domain t1 from sub-experiment to sub-experiment and with the signal intensity acquired for each sub-experiment along one time axis t2 (the acquisition time).
As an example, in the 2D 1H,1H COSY experiment (see abvoe) the second 90o pulse is applied immediately after the first pulse in the first sub-experiment and is then shifted successively along t1 in the course of the subsequent sub-experiments respectively.
In this way - since the state of the investigated spin-system will be varied along t1 in a well-defined way according to the design of the chosen pulse sequence - selected properties of the investigated spin-system such as i.e. its nJHH coupling network may be conveniently evaluated.
Consequently, and since the signal intensity, phase or both these properties depend on two time-axis t1 and t2 two Fourier Transformations have to be performed with 2D raw data.
2D experiments are aimed mainly for the determination of different types of coupling or correlation networks, for improving spectral resolution in general, i.e. for disentangling the signals in overcrowded spectral regions into two frequency domains and for conveniently getting spectral information only hardly obtainable (or even not obtainable at all) with 1D experiments.
The manifold and power of 2D experiments dedicated to and tailored for almost any type of structural problem, which has been designed in the past, is most probably the main reason for the today’s popularity of NMR spectroscopy.
NMR experiments may be grouped according to various criteria, such as the “dimensionality” (1D, 2D, …), the investigated nucleus/nuclei and others.
Note that the dimensionality of NMR experiments is not restricted to 1D and 2D but has been extended to 3D- or even 4D-NMR experiments. These multidimensional experiments have proved to be most valuable for the investigation of biomolecules the complex, highly crowded spectra of which are hardly manageable with 1D and 2D experiments.
BACK TO: |
HOW 2D NMR WORKS
CHECK IT: | Marvel at the following video (BRUKER) demonstrating in short the principle of 2D Correlation Spectroscopy exploited in experiments such as 2D COSY, 2D TOCSY, 2D NOESY and others. Use the link below to access the selection of BRUKER Academy Videos and choose WHAT IS 2D NMR. Note that a registration/login will be requested. Activate full screen mode and start the video. |
 | 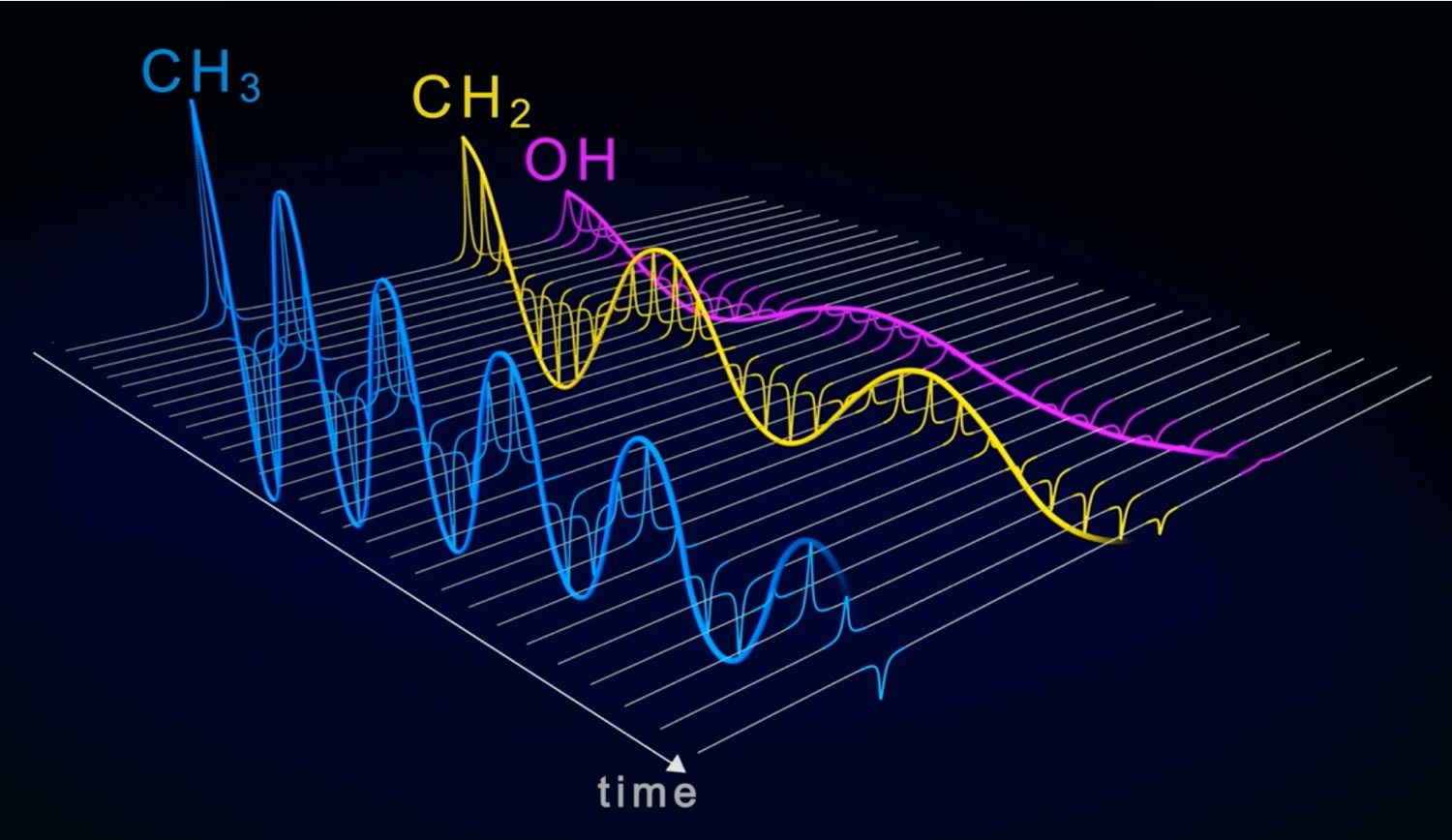 |
BACK TO: |
ANALYSIS AND SIMULATION OF NMR EXPERIMENTS
“All models are approximations.
Essentially, all models are wrong, but some are useful.
However, the approximate nature of the model must always be borne in mind."
George E. P. Box, statistician (1919 - 2013)
Models are used for understanding the mechanics, the dependence on experimental parameters and for the design, the modification and the optimization of NMR experiments.
Several types of models are available and in use with NMR experiments the choice of which depends on the experiment’s complexity and the motivation for the investigation. The choice also depends on the quality of the expected information thereof, whether e.g. the simple visualization or a more comprehensive and quantitative treatment of a pulse sequence is in the focus:
- VECTOR MODEL
- PRODUCT OPERATOR MODEL
- DENSITY MATRIX MODEL
This tutorial is laid-out for users familiar with the basics of NMR as given in introductory lectures on NMR spectroscopy or in corresponding textbooks.
Basic theory therein however, is usually supported solely by the classical vector model. This model relies on magnetizations for a given nucleus I (MIz, MIx, MIz) and its evolution under the influence of chemical shifts, couplings or rf-pulses is described in terms of the Bloch equations based on classical physics.
This model generates an easily to interpret graphical image of the processes in a pulse sequence. However, the classical is only adequate for describing and understanding simple experiments such as the 1D one-pulse 1H or 13C experiments or the inversion-recovery experiment for measuring T1 relaxation times. The model fails with more sophisticated pulse sequences such as 1D 13C DEPT or 2D 1H,1H COSY.
In this tutorial and to yield reliable results close to the outcome of real NMR spectrometers with any kind of 1D and 2D multi-pulse NMR experiments the TOPSPIN NMRSIM module will be used which is based on the rigorous density matrix model.
This quantum-mechanical approach does not deal directly with observable magnetizations, but rather with the state of the spin-system, which is expressed either by the wave function Ψ(t) or by the density operator σ(t).
However, this model although comprehensive and powerful even with complex experiments and when applied to strongly coupled spin systems is not that clear as the vector model and is less suited for direct and easily to interpret analytical outputs. That is why – as with NMRSIM – the density matrix model is typically used to yield numerical outputs, such as the generation of the (numerical) time-domain signal (FID) of a given experiment.
To get a more comprehensive view of a pulse sequence, particularly including the processes within a pulse sequence and to supplement the purely numerical output of NMRSIM the so-called product operator formalism (PO-formalism), yielding analytical results will be used sporadically in the course of the tutorial.
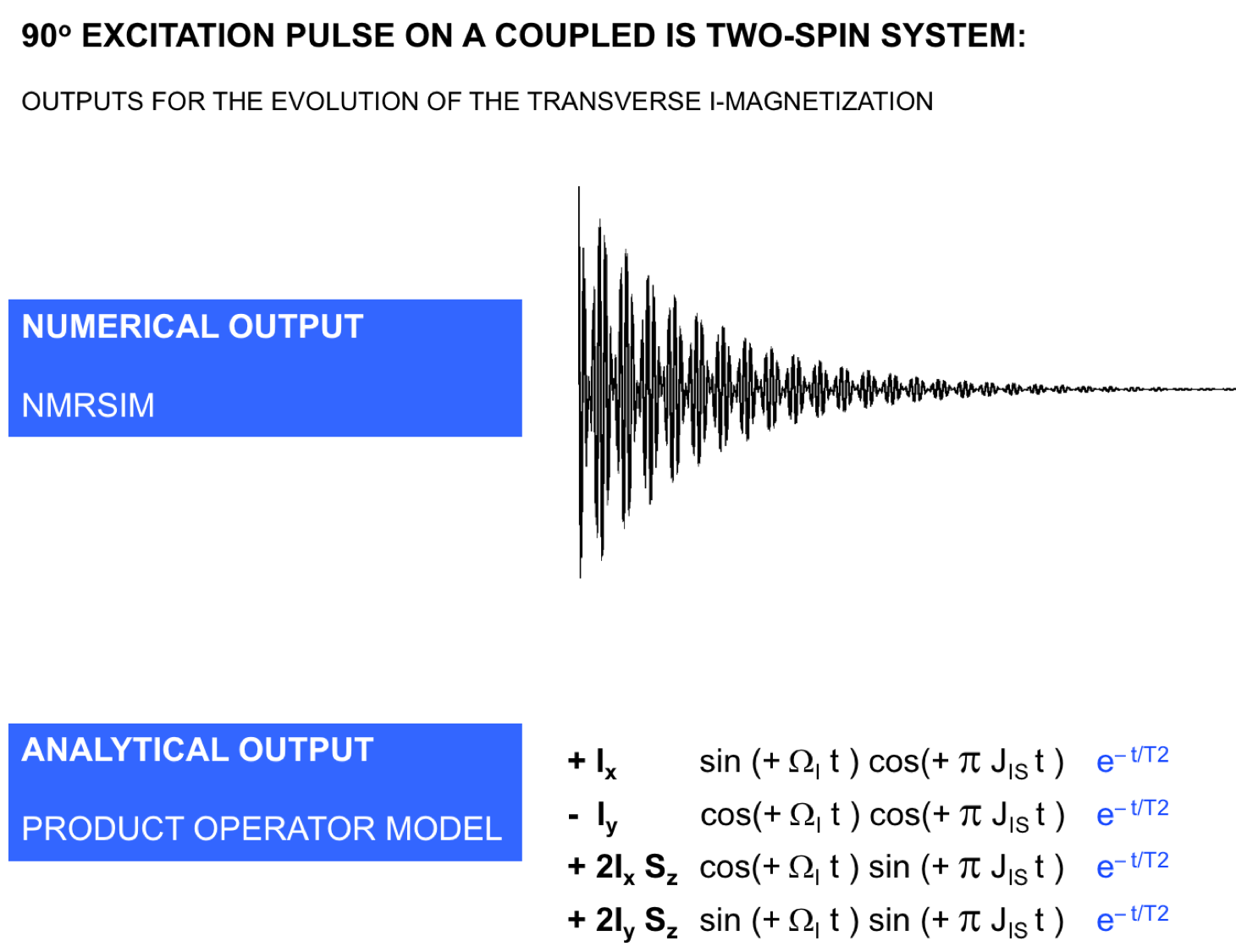
As an example of the two types (numerical/analytical) of results obtained with NMRSIM and the product operator model the output for the evolution (in t) of the transverse magnetization of spin I of a coupled IS-two spin system after a 90ox excitation pulse is given.
Note that with product operators relaxation (the extra terms in blue) will be neglected:
 |
This product operator approach follows the middle course between the vector-model and the rigorous density matrix formalism. It is founded on the density operator theory but retains the intuitive concepts of the classical or semiclassical vector models.
Again, this model deals with the states of a spin-system expressed by different types of product operators such as Iz, Ix, 2IySz which are based on the spin angular momentum. Closely related to Mz, Mx and “anti-phase” My magnetizations respectively in the classical model these product operators can be associated with clear physical meaning.
Typically, weakly coupled spin-systems are assumed, relaxation and related effects (NOE, ROE) are not taken into account.
The effects of chemical shifts, couplings and rf-pulses on these product operators are called “rotations” because of the corresponding (rotation-) rules.
Hence the product operator formalism is not only comprehensive and precise for describing the progress of pulse sequences with a given spin-system but – due to its clearness – is also well suited for the “visual understanding” of this process.
This is demonstrated below (in comparison to the classical vector model) for a single-spin system MIz (Iz) when exposed to a simple echo pulse sequence:
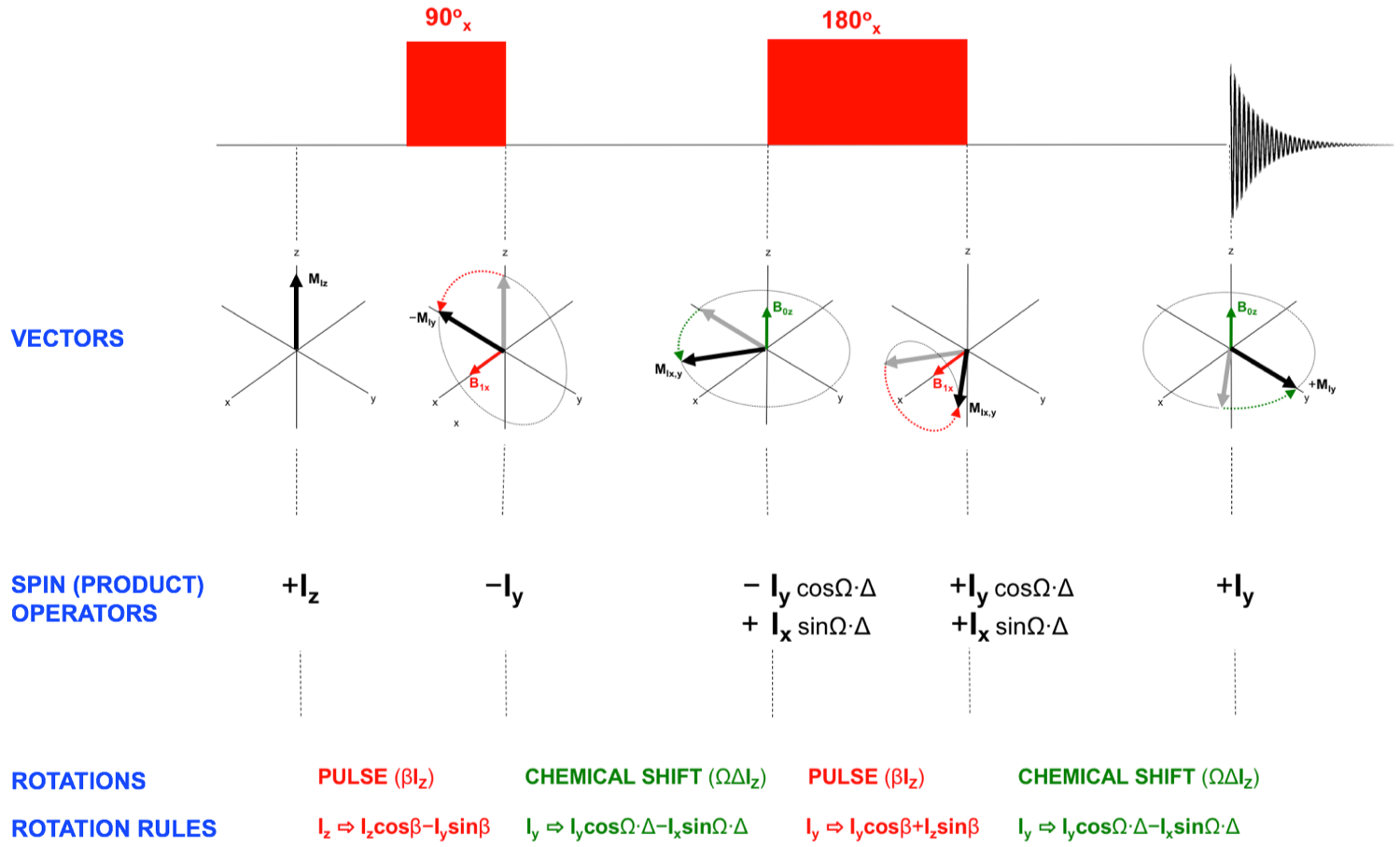 |
This model has proved to be on the one side highly capable for describing precisely the evolution of spin systems under the influence of also more complicated pulse sequences. On the other hand, this model is not a pure “black box” requesting for some inputs and yielding a final output with no insight what is going on “in-between”. Quite the contrary the model allows the user to follow and understand the effect of a pulse sequence step-by-step from the first delay (or pulse) to final data acquisition. Based on analytical expressions the product operator model allows the accurate calculation of values (e.g. signal intensities) from variables (e.g. chemical shift, coupling constant, pulse angle).
At any stage of the pulse sequence the model's prediction (product operator terms) may easily be “translated” into and visualized as spectral properties such as the intensity, the sign and phase of longitudinal and transversal magnetizations, allowing the spectral appearance to be understood at that stage.
Most important the product operator model may be applied taking advantage of two basis, the Cartesian or the Spherical basis. Simple rules allow spin states in the Cartesian basis to be transformed into and expressed in Spherical basis and vice versa.
With the Cartesian basis the progress of a spin system under the influence of a given pulse sequence is expressed step-by-step in terms of Cartesian operators (Ix, 2IxSz, 2IySx etc.). With the Spherical basis progress is studied in terms of coherence levels following the coherence pathway concept.
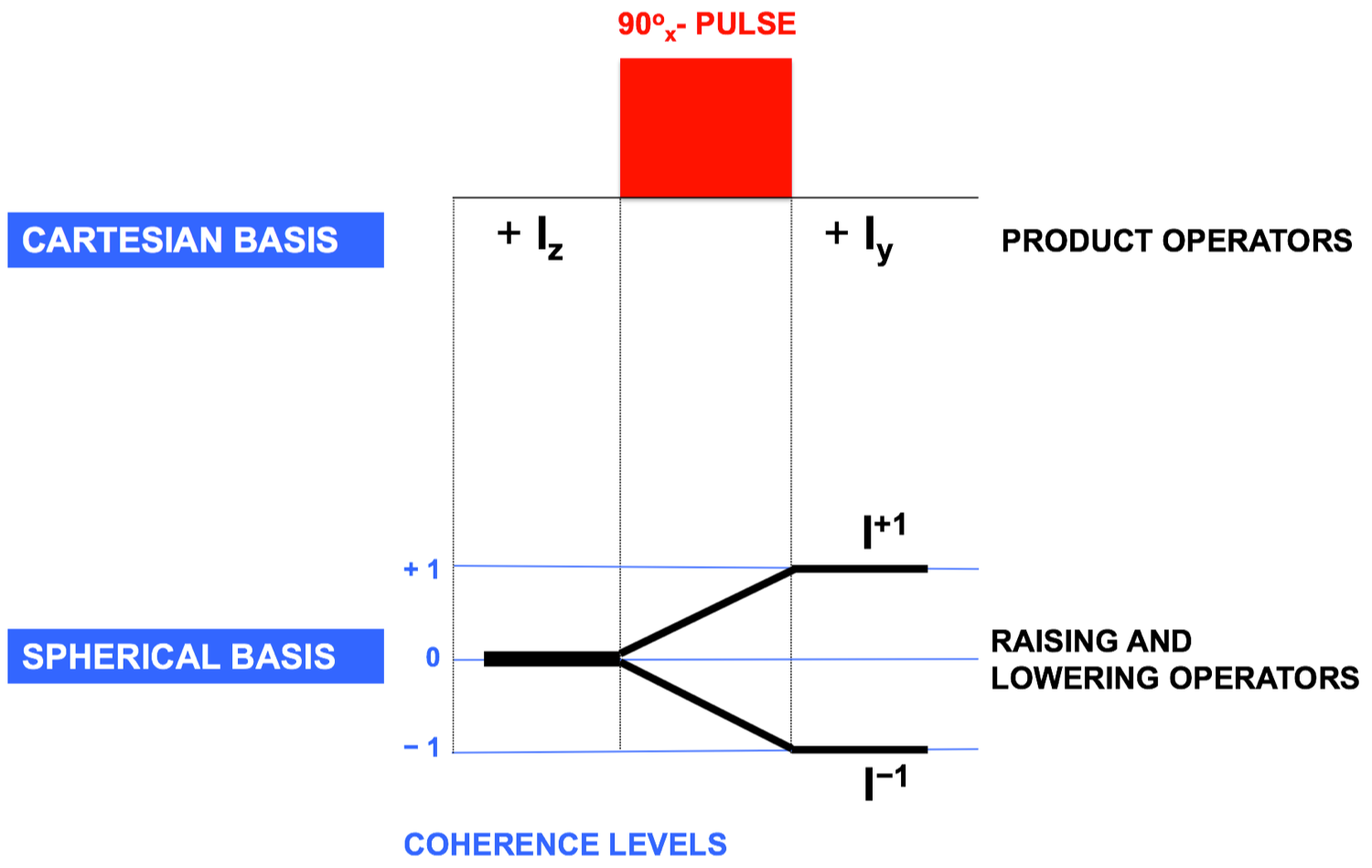 |
Whereas the Cartesian basis yields more detailed information and is typically the basis of choice, the spherical basis has turned out to be indispensable for following and understanding the progress of pulse sequences under the influence of magnetic field gradients which are most common in many NMR experiments. With the transformation rules the state of a spin system (in the Cartesian basis) may be transformed and expressed at any stage of the investigated pulse sequence into the Spherical basis, e.g. to study the effect of magnetic field gradients at that stage.
For the detailed description of the (rotation-) rules governing the progress of a spin system under the influence of chemical shifts, couplings and rf-pulses in the Cartesian basis and of the transformation rules (Cartesian/Spherical basis) the user is referred to one of the references listed below.
BACK TO: |
MORE DETAILED INFORMATION ON THE PRODUCT OPERATOR FORMALISM
To not overburden this part of the tutorial with a more detailed introduction to the product operator formalism a few more rigorous propaedeutic descriptions for interested users are listed below.
Besides a few videos descriptions in the pdf-format are available, which necessitates a corresponding pdf-reader such as the ACROBAT READER:
 | Read more about: ACROBAT READER ACROBAT READER Acess the ADOBE SYSTEMS home page and download the latest version of the ADOBE READER.
PDF-FILES: DOWNLOAD - VIEW - STORAGE PDF-FILES: DOWNLOAD, view, storage Note at this stage that the pdf-files below are located differently:
Therefore - with macOS- and WINDOWS-PCs - adjust the settings of your browser according to your needs:
To archive these pdf-files (and additional downloadable pdf-files appearing below) and to keep together the various other types of files of this tutorial such as NMR data, the reference files or your personal lab report forms establish and use a corresponding directory/subdirectory file tree such as e.g.:
|
Users not familiar with the basics and the application of the product operator model are referred to:
 | the following attractive video-lectures by James Keeler (University of Cambridge, UK) LECTURE (I) ON PRODUCT OPERATORS (48 min) |
 | the following excellent (written) introductions (pdf-files) by James Keeler (University of Cambridge, UK) INTRODUCTION (A) TO THE PRODUCT OPERATOR FORMALISM (pdf) |
 | the Product Operator appendix to a lecture course (pdf) by Peter Bigler (University of Berne, Switzerland) |
the eNMR Encyclopedia (NMR Basics/Product Operator Formalism) accessible through the BRUKER NMR Guide and the references cited therein. |
Note that besides these (and other) introductions and review articles addressing the product operator formalism numerous product operator calculators are available. They are intended to undertake the cumbersome (and error-prone) step-by-step manual calculation which greatly facilitates product operator treatments of more complex pulse sequences with multi-spin systems.
THE PRODUCT OPERATOR PROGRAM SIM3
- SIM3 is an older but very versatile program, written by R.E.D. McClung, University of Alberta, Edmonton, Canada, for simulating NMR pulse sequences using the product operator (PO) formalism.
- unlike most other programs, SIM3 can calculate the stepwise evolution of spin systems under the influence of pulse sequences using product operators in both in the Cartesian and spherical basis.
This "dual approach" allows, on the one hand, the tracking of the evolution in the form of Cartesian operators, which are directly related to the more easily visualized macroscopic magnetizations.
On the other hand, the spherical basis also enables the understanding and efficient modeling of the coherence transfer pathways traversed during a pulse sequence.
The latter is essential for incorporating magnetic field gradients and understanding their influence on a spin system. As will be shown in the following chapters, magnetic field gradients are now an indispensable tool in the development of high-performance pulse sequences. - SIM3 runs on the old DOS operating system. This requires a suitable DOS emulator such as DOSBox.
 | PRODUCT OPERATOR CALCULATOR SIM3 After copying the following zip-file PO-SIMULATION to your PC/MAC, e.g., to your local folder NMR_TUTORIAL a subfolder SIM3, containing the SIM3 program and a few examples, the SIM3-MANUAL and SIM3 WITH DOSBOX, a recipe how to install and start SIM3, will be available.
DOSBox DOSBox is a DOS-emulator that uses the SDL-library which makes DOSBox very easy to port to different platforms.
|
BACK TO: |
ADDITIONAL INFORMATION ON NMR EXPERIMENTS
If interested in a more comprehensive description of NMR experiments in general take a look at the Keeler Group - Lectures Website with a series of experimental topics:
 |
BACK TO: |
ADDITIONAL INFORMATION ON NMR IN GENERAL (APPLICATIONS, EQUIPMENT, TECHNIQUES, ...)
If interested in additional NMR-topics such as NMR-applications, equipment, techniques ....take a look at the BRUKER site Application Notes - Magnetic Resonance with a wealth of information in the form of articles, videos, ...:
 | APPLICATION NOTES - MAGNETIC RESONANCE (BRUKER) Use the Filters and Search options for having access to the desired information. |
BACK TO: |
FORWARD TO: |





